第二章 算法—程序的灵魂

讲师介绍：软件工程师，阿里云技术专家，《智能前端技术与实践》作者

考试科目：883 《C程序设计》（第五版）谭浩强，清华大学出版社

参考资料：《C程序设计（第五版）》谭浩强

前言

算法 = 数据结构 + 程序

一个程序主要包括以下两方面的信息：

• 对数据的描述：在程序中要指定用到哪些数据以及这些数据的类型和数据的组织形式，即数据结构；
• 对操作的描述： 要求计算机进行操作的步骤，即算法；

一个程序设计人员应具备算法、数据结构、程序设计方法以及语言工具四个方面的知识，其中算法是灵魂，数据结构是加工对象，语言是工具，编程需要采用合适的方法。

2.1 什么是算法

1. 定义：广义的说，为解决一个问题而采取的方法和步骤，就称为“算法”，如乐谱、菜谱等；
2. 优缺点分析：从事各种工作和活动，都必须事先想好进行的步骤，然后按部就班地进行，才能避免产生错乱，然而有的方法只需要进行很少的步骤，而有的方法则需要较多的步骤，一般来说，希望采用方法简单、运算步骤少的方法，因此，为了有效地进行解题，不仅需要保证算法正确，还要考虑算法的质量，选择合适的算法；
3. 算法分类：
   • 数值运算算法：求数值解，如求方程的根、求一个函数的定积分，一般有封装好的数学程序库；
   • 非数值运算算法：其应用领域超过数值运算算法，最常见的是用于事务管理领域，如对一批职工按姓名排序、图书检索、人事管理和行车调度等，典型算法包括排序算法、查找算法等；

2.2 简单算法举例

例题2.1：求1 X 2 X 3 X 4 X 5

#include<stdio.h>
int main(){
    int num,temp = 1;
    printf("请输入num数值：");
    scanf("%d",&num);
    if(num>=0){
        for(int i = 1;i <= num;i++){
            temp *= i;
        }
        printf("%d的阶乘值为：%d\n",num,temp);
    }else{
        printf("请重新输入num数值！");
    }
    return 0;
}

例题2.2：求1 X 2 X 4 X 6 X 8

• 方法一：通过修改自加运算的步幅；

  • 求偶数乘积

  #include<stdio.h>
  int main(){
      int num,temp = 1;
      printf("请输入num数值：");
      scanf("%d",&num);
      if(num>=0){
          for(int i = 2;i <= num;i += 2){
              temp *= i;
          }
          printf("%d以内偶数的阶乘值为：%d\n",num,temp);
      }else{
          printf("请重新输入num数值！");
      }
      return 0;
  }
  

  • 求奇数

  #include<stdio.h>
  int main(){
      int num,temp = 1;
      printf("请输入num数值：");
      scanf("%d",&num);
      if(num>=0){
          for(int i = 1;i <= num;i += 2){
              temp *= i;
          }
          printf("%d以内奇数的阶乘值为：%d\n",num,temp);
      }else{
          printf("请重新输入num数值！");
      }
      return 0;
  }
  

• 方法二：

#include<stdio.h>
int main(){
    int num,temp = 1;
    printf("请输入num数值：");
    scanf("%d",&num);
    if(num>=0){
        for(int i = 1;i <= num;i++){
            if(i%2==0){
                temp *= i;
            }
        }
        printf("%d以内偶数的阶乘值为：%d\n",num,temp);
    }else{
        printf("请重新输入num数值！");
    }
    return 0;
}

例题2.3：判定2000～2500年中的每一年是否为闰年，并将结果输出。

判断是否为闰年的条件：

• 能被4整除，不能被100整除；
• 能被400整除；

 #include <stdio.h>
 int main(){
     printf("2000年～2500年中的闰年年份包括：\n");
     for(int a = 2000;a <= 2500;a++){
         if((a%4==0&&a%100!=0)||(a%400==0)){
            printf("%d\n",a);
         }
     }
     return 0;
 }

例题2.4：求1- (1/2 ) + (1/3) - (1/4) + ...。

#include<stdio.h>
int main(){
    int num;
    double result = 0.0;
    printf("请输入num值：");
    scanf("%d",&num);
    if(num>=0){
        for (int i = 1; i <= num; i++) {
            if(i%2==1){
                result += 1.0/i;
            }else{
                result -= 1.0/i;
            }
        }
        printf("最终结果为：%f\n",result);
    }else{
        printf("请重新输入num值！\n");
    }
    return 0;
}

例题2.5：判断素数。

所谓素数，是指除了1和该数本身之外，不能被其他任何整数整除的数，因此判断一个数（数n，n>=3）是否为素数的方法就是：将2~n-1各个整数先后作为除数，如果都不能被整除，则n为素数。

• 方法一：

#include<stdio.h>
int main(){
    int i,j=2,flag=true;
    printf("请输入一个数字：");
    scanf("%d",&i);
    for (; j<i; j++) {
        if(i%j==0){
            flag = !flag;
          	break;
        }
    }
    if(flag){
        printf("%d是一个素数\n",i);
    }else{
        printf("%d不是一个素数\n",i);
    }
    return 0;
}

• 方法二：

#include<stdio.h>
int main(){
    int i,j=2,flag=true;
    printf("请输入一个数字：");
    scanf("%d",&i);
    for (; j<i/2; j++) {
        if(i%j==0){
            flag = !flag;
            break;
        }
    }
    if(flag){
        printf("%d是一个素数\n",i);
    }else{
        printf("%d不是一个素数\n",i);
    }
    return 0;
}

2.3 算法的特性

一个有效的算法应该包含应该具有以下几个特点：

• 有穷性：一个算法应该包含有限的操作步骤，而不能是无限的；
• 确定性：算法中的每一步应当都是确定的，而不应该是含糊的、模棱两可的；
• 有零个或多个输入：所谓输入是指在执行算法时需要从外界取得必要的信息；
• 有一个或多个输出：算法的目的是为了“求解”，“解”就是输出；
• 有效性：算法中的每一个步骤都应该能有效的执行，并得到确定的结果（如a/0始终有效执行）；

2.4 怎样表示一个算法

2.4.1 用自然语言表示算法

自然语言就是人们日常使用的语言，可以是汉语、英语或其他语言，用自然语言通俗易懂，但文字冗长，容易出现歧义。

2.4.2 用流程图表示算法

流程图示用一些图框来表示各种操作，用图形表示算法，直观形象，易于理解。

「例题2.5 判断素数」的流程图如下所示：

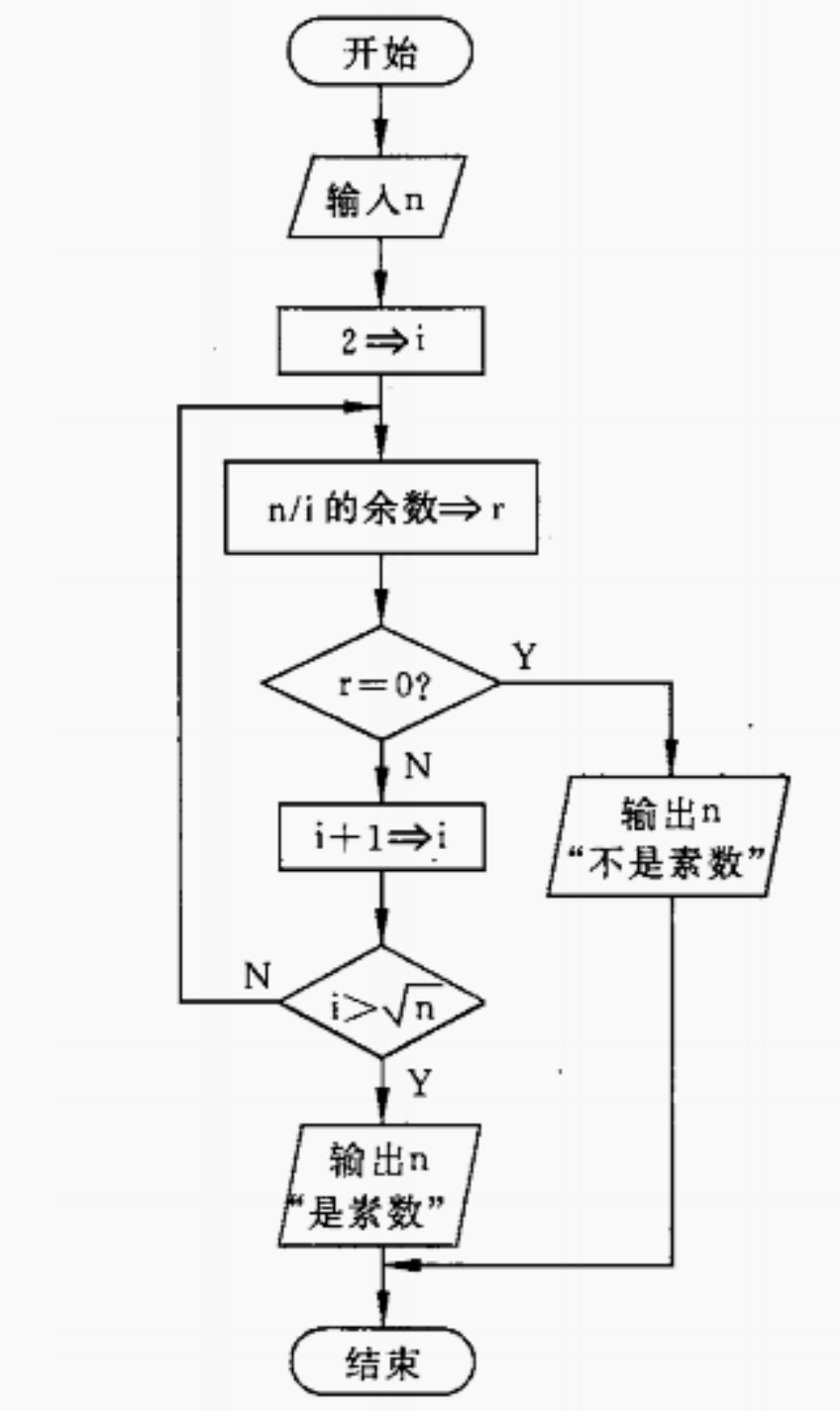
2.4.3 三种基本结构和改进的流程图

传统的流程图用流程线指出各框的执行顺序，对流程线的使用没有严格限制。因此，使用者可以不受限制地使流程随意地转来转去，使流程图变得毫无规律，阅读时要花很大精力去追踪流程，使人难以理解算法的逻辑。

三种基本结构：

• 顺序结构：

  如图所示，虚线框内是一个顺序结构，其中A和B两个框是顺序执行的，即：在执行完A框所指定的操作之后，必然接着执行B框所指定的操作，顺序结构是最简单的一种基本结构。

  

• 选择结构：

  选择结构又称选取结构或分支结构，如图所示，虚线框内是一个选择结构，此结构中必包含一个判断框，根据给定的条件p是否成立而选择执行A框或B框。

  

  【注】：无论p条件是否成立，只能执行A框或B框之一，不可能既执行A框又执行B框，无论走哪一条路径，在执行完A或B后，都经过b点，然后脱离本选择结构，A或B两个框中可以有一个是空的，即不执行任何操作，如图所示：

  

• 循环结构：

  • 当型（while型）循环结构：当给定的条件p1成立时，执行A框操作，执行完A后，再判断条件p1是否成立，如果仍然成立，再执行A框，如此反复执行A框，直到某一次p1条件不成立为止，此时不执行A框，而从b点脱离循环结构；

    

  • 直到型（until型）循环结构：先执行A框，然后判断给定的p2条件是否成立，如果p2条件不成立，则再执行A，然后再对p2条件作判断，如果p2条件仍然不成立，又执行A......如此反复执行，直到给定的p2条件成立为止，此时不再执行A，从b点脱离本循环结构；

由以上3种基本结构顺序组成的算法结构，可以解决任何复杂的问题。由基本结构所构成的算法属于“结构化”的算法，它不存在无规律的转向，只在基本结构内才允许存在分支和向前或向后的跳转。

2.4.4 用N-S流程图表示算法

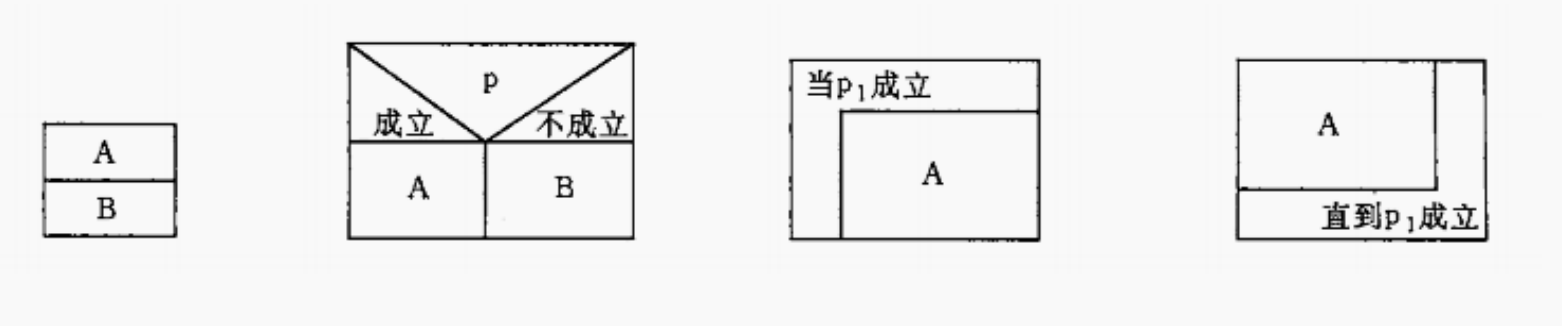
既然用基本结构的顺序组合可以表示任何复杂的算法结构，那么，基本结构之间的流程线就属多余的了。将全部算法写在一个矩形框内，在该框内还可以包含其他从属于他的框，或者说，由一些基本的框组成一个大的框，这种流程图又称N-S结构化流程图，其符号如图所示：（由左至右依次为：顺序结构、选择结构、当型循环结构、直到型循环结构）

2.4.5 用伪代码表示算法

伪代码是介于自然语言和计算机语言之间的文字和符号来描述算法，用伪代码写算法并无固定的、严格的语法规则，可以用英文，也可以中英文混用，只要把意思表达清楚，便于书写和阅读即可，书写的格式要写成清晰易读的形式。

例题2.6 求5!的伪代码

begin(算法开始)
  1=>t
  2=>i
  while i<=5
  {
    	t*i=>t
      i+1=>t
  }
	print t
end(算法结束)

2.4.6 用计算机语言表示算法

要完成一项工作，包括设计算法和实现算法两个部分，只有用计算机编程语言编写的程序写才能被计算机执行，用计算机语言表示算法必须严格遵循所用的语言的语法规则。

2.5 结构化程序设计方法

一个结构化程序就是用计算机语言表示的结构化算法，用3种基本结构组成的程序必然是结构化的程序，这种程序便于编写、阅读、修改和维护，这就减少了程序出错的机会，提高了程序的可靠性，保证了程序的质量。

结构化程序设计方法的基本思路是：把一个复杂问题的求解过程分阶段进行，每个阶段处理的问题都在人们容易理解和处理的范围内，具体来说，采取以下方法来保证得到结构化的程序：

• 自顶向下
• 逐步细化
• 模块化设计
• 结构化编码